こちらの公立春日井小牧看護専門学校の過去問の解答・解説は、同校を受験する受験生のためにアイプラスアカデミーが作成した過去問の解答・解説です。
公立春日井小牧看護専門学校の一般入試を受験するみなさんの直前対策にご活用ください!
目次
公立春日井小牧看護専門学校 過去問(令和5年度一般入試) 数学 解答・解説
[1]大問1
(1)
解答:$(3x+4)(2x-3)$
解説:たすき掛けの因数分解
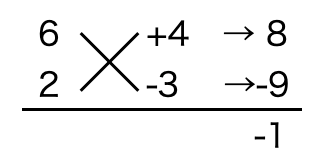
(2)
解答:6
解説:${a+\frac{1}{a}=\frac{1}{\sqrt{2}-1}+\frac{\sqrt{2}-1}{1}=\frac{\sqrt{2}+1}{2-1}+\sqrt{2}-1=\sqrt{2}+1+\sqrt{2}-1=2\sqrt2}$
また、${a^2+\frac{1}{a^2}=\left(a+\frac{1}{a}\right)^2-2\times{a}\times\frac{1}{a}=\left(a+\frac{1}{a}\right)^2-2}$となるので、
${a^2+\frac{1}{a^2}=\left(a+\frac{1}{a}\right)^2-2=(2\sqrt2)^2-2=8-2=6}$
[2]大問2
(1)
解答:${6\sqrt3}$
解説:一辺が2の正六角形は、一辺が2の正三角形6つからできている。
1つの三角形の面積は${\frac{1}{2}\times2\times\sqrt3=\sqrt3}$
よって、この正六角形の面積は${\sqrt3\times6=6\sqrt3}$
(2)
解答:12
解説:向かい合う頂点を結んだ対角線3本のそれぞれの長さは${4}$
2つ隣の頂点と結んだ6本の対角線の長さは${2\sqrt3}$
よって、9個の対角線の長さの和は${4\times3+2\sqrt3\times6=12+12\sqrt3}$
したがって、${x}$の値は${12}$
[3]大問3
(1)
解答:2
解説:${y=2x^2+4x-1=2(x+1)^2-3}$より、頂点の座標は${(-1,-3)}$
よって、${p-q=(-1)-(-3)=2}$
(2)
解答:1
解説:${y=2x^2-6x=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}}$より、このグラフの頂点は
${\left(\frac{3}{2},-\frac{9}{2}\right)}$${y=2x^2+4x-1}$の頂点が${(-1,-3)}$であるので、
${x}$軸方向に移動した${m=\frac{3}{2}-(-1)=\frac{5}{2}}$
${y}$軸方向に移動した${n=-\frac{9}{2}-(-3)=-\frac{3}{2}}$
よって、${m+n=\frac{5}{2}+\left(-\frac{3}{2}\right)=1}$
[line_friends_content]
[4]大問4
(1)
解答:8
解説:2130を素因数分解すると、${2160=2^43^35^1}$
よって、${p=4,q=3,r=1}$したがって、${p+q+r=4+3+1=8}$
(2)
解答:40
解説:1350を素因数分解すると、${1350=2^13^35^2}$
よって、${2160=2^43^35^1}$との最大公約数${G=2^13^35^1}$
また、最小公倍数${L=2^43^35^2}$
したがって、${\frac{L}{G}=\frac{2^43^35^2}{2^13^35^1}=2^35^1=40}$
[5]大問5
(1)
解答:25
解説:食塩水の濃度は${\frac{食塩の量(g)}{食塩水の量(g)}\times{100}}$
いま食塩20グラムと水60グラムを混ぜたので、食塩水の量は80グラム
したがって、${\frac{20}{80}\times{100}=25}$(%)
よって、${x=25}$
(2)
解答:225
解説:300円の2割5分は${300\times\frac{2.5}{10}=75}$
これを300円から引くので、${x=300-75=225}$
[6]大問6
(1)
解答:${-t^2+t+1}$
解説:${cos^2θ=1-sin^2θ}$より、${cos^2θ+sinθ=(1-sin^2θ)+sinθ=-sin^2θ+sinθ+1}$
よって、${sinθ=t}$とおくと、${-t^2+t+1}$
(2)
解答:${\frac{1}{4}}$
解説:(1)の${-t^2+t+1}$を利用する。${0^\circ≦θ≦180^\circ}$のとき、${0≦t≦1}$
${y=-t^2+t+1}$の頂点は${\left(\frac{1}{2},\frac{5}{4}\right)}$なので、
${t=\frac{1}{2}}$のとき最大値${M=\frac{5}{4}}$をとる。
また、${t=0,1}$のとき最小値${m=1}$をとる。
よって、${M-m=\frac{5}{4}-1=\frac{1}{4}}$
[7]大問7
(1)
解答:${\frac{16}{625}}$
解説:4回引いて3回だけ当たりくじを引く引き方は、${_4C_3}$通り
1回くじを引いたとき、
当たりが出る確率は${\frac{2}{10}=\frac{1}{5}}$
はずれが出る確率は${\frac{8}{10}=\frac{4}{5}}$
よって、求める確率は${_4C_3\times\left(\frac{1}{5}\right)^3\times\left(\frac{4}{5}\right)=\frac{16}{625}}$
(2)
解答:${\frac{369}{625}}$
解説:4回引いて当たりくじを1回も引かない確率は${\left(\frac{4}{5}\right)^4=\frac{256}{625}}$
よって、少なくとも1回は当たりくじを引く確率は${1-\frac{256}{625}=\frac{369}{625}}$
[8]大問8
(1)
解答:20
解説:${a,b,c}$の目の組み合わせは6つの目から3つを選べばいいので、${_6C_3=20}$通り
(2)
解答:189
解説:${a,b,c}$のすべてが奇数となるのは、${3^3=27}$通り
よって、${a,b,c}$のすべての目の出かたは${6^3=216}$
したがって、${a,b,c}$の少なくとも1つが偶数となる場合は、${216-27=189}$
[9]大問9
(1)
解答:-3
解説:データを昇順に並べ替えると20, 30, 30, 30, 50, 50, 60, 60, 70, 70
よって、中央値${m=\frac{50+50}{2}=50}$
平均値${n=\frac{1}{10}\times{(20+30+30+30+50+50+60+60+70+70)}=47}$
したがって、${n-m=47-50=-3}$
(2)
解答:15
解説:第一四分位数は30、第三四分位数は60
よって、四分位偏差は${\frac{60-30}{2}=15}$
[10]大問10
(1)
解答:${\sqrt2}$
解説:${cos\angle{BAC}=-\frac{1}{3}}$より、${sin\angle{BAC}=\frac{2\sqrt2}{3}}$
よって、三角形ABCの面積は、${\frac{1}{2}\times3\times1\times{sin\angle{BAC}}=\sqrt2}$
(2)
解答:${\frac{9\sqrt2}{2}}$
解説:余弦定理より、${BC^2=AB^2+CA^2-2\times{AB}\times{CA}\times{cos\angle{BAC}}}$
よって、${a^2=9+1-6\times\left(-\frac{1}{3}\right)=12}$
${a>0}$なので、${a=2\sqrt3}$
また、外接円の半径Rは、正弦定理より、${\frac{BC}{sin\angle{BAC}}=2R}$
よって、${\frac{2\sqrt3}{\frac{2\sqrt2}{3}}=2R}$${\frac{2\sqrt2}{3}\times2R=2\sqrt3}$
したがって、${R=2\sqrt3\times\frac{3}{4\sqrt2}=\frac{3\sqrt6}{4}}$
以上より、aとRの積は${a\times{R}=2\sqrt3\times\frac{3\sqrt6}{4}=\frac{9\sqrt2}{2}}$
[/line_friends_content]